Wave
Mechanics and IYQ25
Pioneers of Quantum Theoretical Physics – Part 4
Louis de Broglie, Erwin Schrödinger & Max Born
An ocean traveller
has even more vividly the impression that the ocean is made of waves than that
it is made of water.
-
Arthur Eddington
Probability density distribution for an electron
UNESCO has proclaimed 2025 as the International Year of Quantum Science and Technology (IYQ). This year-long, worldwide initiative will celebrate the contributions of quantum science to technological progress over the past century, raise global awareness of its importance to sustainable development in the 21st century, and ensure that all nations have access to quantum education and opportunities.
In celebration of IYQ25, this series of articles focuses on the key personalities of quantum theoretical physics and their work – ten of the greatest, from Planck to Feynman. This is the fourth article in the series and focuses on the development of Wave Mechanics through the contributions of Louis de Broglie, Erwin Schrödinger and Max Born. For the earlier articles in this series, see 1,2,3.
Introduction
Wave mechanics is a foundational branch of quantum mechanics that describes the wave-like behavior of particles. Its development involved key contributions from Louis de Broglie, Erwin Schrödinger, Max Born and others that revolutionized our understanding of atomic and subatomic phenomena.
To trace the early foundations of wave-particle duality, we need to start from Huygens' Wave Theory (1678). Christiaan Huygens proposed that light propagates as a wave, contradicting Newton’s particle theory. According to Huygens’ principle: every point on a wavefront acts as a source of secondary spherical wavelets (see illustration below).
In 1801, Thomas Young demonstrated light interference (see illustration below), supporting the wave nature of light. Further experimental evidence consolidated this picture of light, in apparent conflict with Newton’s particle picture.
As described in a previous article in this series (see
here), Albert Einstein proposed in 1905 that
light also behaves as discrete packets of energy (photons), reintroducing
particle-like properties. This wave-particle duality became crucial for quantum
mechanics as we shall see below and in future articles of this series.
Louis de Broglie’s Bold Proposition
In 1924, French physicist Louis de Broglie made a revolutionary proposal that forever changed our understanding of quantum mechanics. He suggested that all matter exhibits wave-like properties, not just light, which was already known to have both particle and wave characteristics. This idea, though initially met with skepticism, was later confirmed experimentally and became a cornerstone of quantum theory.
De Broglie was deeply influenced by two key developments in early 20th-century physics: (1) Max Planck’s quantum hypothesis (1900) according to which energy is quantized and emitted in discrete packets called quanta, and (2) Albert Einstein’s photon theory (1905) according to which light behaves both as a wave (interference, diffraction) and as a particle (photoelectric effect).
These ideas led de Broglie to ponder: If light (traditionally a wave) has particle properties, could matter (traditionally particles) have wave properties?
In his doctoral thesis (1924), "Recherches sur la théorie des quanta", de Broglie proposed that every moving particle is associated with a wave, and the wavelength (λ) is given by:
λ = h/p
where h is Planck’s constant and p is
the particle’s momentum (mass times the speed). This implied that macroscopic
objects (like a cricket ball) have extremely small wavelengths, making wave
effects negligible. However, microscopic particles (like electrons, protons and
neutrons) have detectable wavelengths.
Why was the idea considered bold? At the time, matter was understood purely in terms of particles. Wave-particle duality was only accepted for light, not matter. Also, no experimental evidence supported matter waves. De Broglie’s proposal was initially seen as speculative, with little enthusiasm from the scientific community. His doctoral thesis was also left in limbo. Soon, it received support from a person who mattered most – Einstein who, recognizing the significance of de Broglie’s work, supported the idea, and this helped gain attention from other physicists. In this respect, Einstein’s intervention helped de Broglie’s career take off the same way that happened a little earlier to Satyendra Nath Bose in India (see here).
Experimental confirmation
The most decisive experimental validation of de Broglie’s idea of the wave nature of particles came from American physicists Clinton Davisson and Lester Germer at Bell Labs in 1927. They fired a beam of electrons at a nickel crystal and observed a diffraction pattern (a hallmark of wave behavior) in the scattered beam (see illustration below). The pattern matched the predictions of de Broglie’s formula (λ = h/p), confirming that electrons exhibit wave-like behavior, just like light.
An independent confirmation came from Thomson’s experiments later (also in 1927). British physicist George Paget Thomson (son of the famous J J Thomson, discoverer of the electron) independently demonstrated electron diffraction using thin metal foils (see illustration below), further validating de Broglie’s hypothesis.
For their work, Davisson and Thomson shared the 1937 Nobel Prize in Physics.
Louis de Broglie (1892 - 1987) – a biographical sketch
Louis Victor Pierre Raymond, 7th Duc de Broglie was the second son of a member of the French nobility. From the Broglie family, whose name is taken from a small town in Normandy, have come high-ranking soldiers, politicians, and diplomats since the 17th century. In choosing science as a profession, Louis de Broglie broke with family tradition, as had his brother Maurice (from whom, after his death, Louis inherited the title of duke). Maurice, who was also a physicist and made notable contributions to the experimental study of the atomic nucleus, kept a well-equipped laboratory in the family mansion in Paris. Louis occasionally joined his brother in his work, but it was the purely conceptual side of physics that attracted him. He described himself as “having much more the state of mind of a pure theoretician than that of an experimenter or engineer, loving especially the general and philosophical view.” He was brought into one of his few contacts with the technical aspects of physics during World War I, when he saw army service in a radio station on the Eiffel Tower.
De Broglie’s interest in what he called the “mysteries” of atomic physics—namely, unsolved conceptual problems of the science—was aroused when he learned from his brother about the work of the German physicists Max Planck and Albert Einstein, but the decision to take up the profession of physicist was long in coming. He began at 18 to study theoretical physics at the Sorbonne, but he was also earning his degree in history (1909), thus moving along the family path toward a career in the diplomatic service. After a period of severe conflict, he declined the research project in French history that he had been assigned and chose for his doctoral thesis a subject in physics.
In 1924, he published his doctoral thesis, which introduced the concept of matter waves, leading to the formulation of the de Broglie wavelength. This revolutionary idea laid the foundation for the development of wave mechanics and significantly influenced the work of other prominent physicists, including Erwin Schrödinger and Niels Bohr.
For his contributions to quantum physics, de Broglie was awarded the Nobel Prize in Physics in 1929. Throughout his career, he continued to explore the implications of his theories and engaged in philosophical discussions about the nature of reality and the (Copenhagen) interpretation of quantum mechanics.
Wave Function
The concept of wave function is central to quantum physics. It is a mathematical function (usually complex-valued) that describes the quantum state of a particle or system. It depends on position (x) and time (t):
y (x, t)
It does not represent a physical wave (like sound or water waves) but instead a probability amplitude.
Interpretation
As we shall discuss in more detail later, in 1926 Max Born proposed that the square of the wave function’s magnitude gives the probability density of finding a particle at a given position (x) and time (t):
P (x, t) = çy2 (x, t) ç
The right-hand side is always a positive quantity irrespective of the nature of the wave function. This connects the abstract wave function to measurable probabilities.
The wave function is the core mathematical object in quantum mechanics, encoding probabilities, dynamics (via Schrödinger’s equation), and quantum weirdness (superposition, entanglement). While its physical meaning is still debated, its predictive power is unmatched.
Schrödinger Wave Equation
In 1926, Erwin Schrödinger came up with the quantum analogue of Newton’s laws of motion in classical physics as follows:
The Schrodinger equation describes how the wave function evolves in space and time and plays the same role in quantum mechanics as Newton’s second law does in classical mechanics. The following is a time-independent (simplified) version of the above:
[The lay reader who may find it difficult to follow these mathematical descriptions may find it prudent to skip them.]
Superposition Principle: Quantum states can be added together to give superposed states, leading to outcomes like ‘quantum interference’ (e.g., double-slit experiment cited above).
Quantization & Eigenstates: The wave function must satisfy appropriate boundary conditions, leading to quantized energy levels (e.g., in atoms).
Solutions to the Schrödinger equation often take the form of eigenstates (stationary states with definite energy):
As we shall see in the next article in this series, Heisenberg’s Uncertainty Principle is central to quantum science – for instance, a sharply localized ψ has a broad momentum distribution, and vice versa.
Erwin Schrödinger (1887 - 1961) – a biographical sketch
Erwin Rudolf Josef Alexander Schrödinger (1887–1961) was an Austrian physicist renowned for his foundational contributions to quantum mechanics, most notably the Schrödinger equation, which describes how quantum systems evolve over time. Born in Vienna on August 12, 1887, Schrödinger was raised in a cultured household with strong interests in science, philosophy, and the arts. He studied physics at the University of Vienna, and graduated in 1910.
Schrödinger’s most famous work came in 1926 when he formulated wave mechanics, an alternative formulation of quantum theory to Werner Heisenberg’s matrix mechanics (to be discussed in the next article in this series). His equation, Ĥψ = Eψ, became a cornerstone of quantum physics, earning him the Nobel Prize in Physics in 1933* (shared with Paul Dirac). Beyond quantum mechanics, Schrödinger explored thermodynamics, statistical mechanics, and color theory. His later years were marked by deep philosophical inquiries into the nature of consciousness, reality, and biology, culminating in his influential 1944 book "What Is Life?", which inspired future work in molecular biology and genetics.
Schrödinger’s Cat: In 1935, Schrödinger proposed his famous "Schrödinger’s Cat" paradox to illustrate the absurdity of applying quantum superposition to macroscopic objects. The scenario is as follows:
A cat is placed in a sealed box with a radioactive
atom, a Geiger counter, a vial of poison, and a hammer. If the
atom decays (a quantum event with a 50% probability in a given time), the
Geiger counter detects it, triggering the hammer to break the poison vial,
killing the cat. Until the box is opened, quantum mechanics suggests that the
atom exists in a superposition—both decayed and not decayed—meaning the cat is
simultaneously alive and dead (see illustration below):
Schrödinger did not actually believe a cat could be both alive and dead. Instead, he was criticizing the Copenhagen Interpretation of quantum mechanics (championed by Niels Bohr and Werner Heisenberg), which claimed that a quantum system remains in superposition until observed. Schrödinger found this idea ridiculous when scaled up to everyday objects like cats.
The paradox has led to multiple interpretations of quantum mechanics.
Schrödinger’s Cat remains a cornerstone of quantum philosophy, illustrating the weirdness of quantum mechanics while pushing physicists to refine their theories. It also influences discussions in philosophy of mind, determinism, and the nature of reality.
Schrödinger’s worldview was profoundly shaped by eastern philosophy, particularly Hindu Vedanta and Buddhist thoughts. His exposure to Indian philosophy came through readings of ancient texts like the Upanishads and the Bhagavad Gita. Schrödinger explicitly linked Eastern mysticism with modern physics, arguing that the Upanishadic idea of universal oneness was compatible with the unified field theories he sought in physics.
Later Years and Legacy: After fleeing Nazi Germany due to his opposition to the regime, Schrödinger settled in Dublin, Ireland, where he became the Director of the School for Theoretical Physics at the Dublin Institute for Advanced Studies (1940–1956) at the special initiative of the Irish prime minister Eamon de Valera, himself a mathematician. He continued writing on philosophy, science, and the intersections between Eastern thought and Western physics until his death in 1961 in Austria.
Schrödinger remains a towering figure in both physics and philosophy, bridging the gap between science and spirituality. His openness to Oriental philosophies distinguished him from many of his contemporaries, making him a unique voice in the dialogue between eastern metaphysics and modern science.
A galaxy of quantum physicists
Max Born’s Probabilistic Interpretation (1926)
Before Max Born’s 1926 breakthrough, Schrödinger’s wave equation (ψ) was seen as describing a physical wave, analogous to classical waves (e.g., sound or water waves). However, this led to paradoxes: If ψ represented an electron’s physical spread, why did experiments detect point-like particles? How could wave interference (e.g., in the double-slit experiment) coexist with discrete particle impacts?
Max Born proposed that |ψ(x)|² (the square of the wave function’s amplitude) gives the probability density of finding a particle at position x. This reconciled wave-particle duality by treating ψ as a probability amplitude rather than a physical wave.
Born was influenced by Einstein’s work on statistical photon behavior (1905), suggesting light quanta behave probabilistically, and scattering experiments where particles appeared at random positions despite wave-like patterns. His critical insight was that the motion of particles follows probability laws, but the probability itself propagates according to causal wave mechanics. This meant that ψ evolves deterministically via Schrödinger’s equation, but measurement outcomes are probabilistic, with |ψ|² giving likelihoods.
Below is an illustration of the methodology of Born’s probabilistic interpretation of the wave function:
Adapted from: https://slideplayer.com/slide/12957367/
Below is a simple example of the application of Born’s probabilistic interpretation of hydrogen wave functions:
From: https://physicsmax.com/wp-content/uploads/2014/08/137.jpg
Max Born (1882 - 1970) – A biographical sketch
Max Born was born on December 11, 1882, in Breslau, Germany (now Wrocław, Poland) into an assimilated Jewish family; his father, Gustav Born, was a professor of anatomy and embryology at the University of Breslau, and his mother, Margarete (Gretchen) Kaufmann, came from a wealthy industrial family.
Born displayed an early aptitude for mathematics and science. He attended the König-Wilhelm-Gymnasium in Breslau before enrolling at the University of Breslau in 1901, where he studied physics, mathematics, astronomy, and philosophy. He later transferred to the University of Göttingen, then a leading center for mathematics and physics, where he studied under prominent figures like David Hilbert, Felix Klein, and Hermann Minkowski. He earned his doctorate in 1907.
After completing his doctorate, Born worked at Cambridge University under J J Thomson but was unimpressed by the experimental focus there. He returned to Göttingen and collaborated with Minkowski on relativity theory. In 1912, he began working on lattice dynamics (the theory of crystal vibrations), a foundational contribution to solid-state physics.
In 1919 he was appointed professor at the University of Frankfurt, where he worked with Otto Stern on experimental quantum theory. In 1921, he succeeded Peter Debye as professor of theoretical physics at the University of Göttingen, turning it into a leading center for quantum mechanics, attracting many of the most brilliant minds in physics of that time, including Heisenberg and Pauli.
In 1925, he collaborated with Werner Heisenberg, Pascual Jordan, and Wolfgang Pauli in formulating matrix mechanics (1925), an early version of quantum mechanics, and mentored future luminaries like Robert Oppenheimer, Maria Goeppert-Mayer, and Enrico Fermi.
After the Nazi rise to power in 1933, being Jewish, Born was forced to leave Germany. He moved to the University of Cambridge, then to Edinburgh University* (1936), where he became a professor and later a British citizen. He Continued work on quantum theory, optics, and nonlinear electrodynamics. After retiring in 1953, he returned to Germany, settling in Bad Pyrmont, and remained active in scientific and philosophical debates.
[* Prior to this he spent six months at the Indian Institute of Science, Bangalore, on the invitation of Indian Nobel Laureate C V Raman with whom he ended up having a frosty relationship.]
He shared the 1954 Nobel Prizer with Walther Bothe for his fundamental contributions to quantum mechanics, particularly the probabilistic interpretation of the wave function. It was an honor long overdue. Many of his students (Heisenberg, Pauli, Fermi) had already become Nobel laureates, cementing his influence on 20th-century physics.
Born married Hedwig (Hedi) Ehrenberg in 1913; they had three children, including Gustav Born, a noted pharmacologist, and Irene Born, who married physicist Sir Maurice Pryce.
He died on January 5, 1970, in Göttingen, Germany.
His Atomic Physics (1935) is one of the most widely used textbooks on the subject, worldwide.
Max Born’s work laid the foundation for modern quantum mechanics, influencing fields from solid-state physics to quantum chemistry. Despite initial resistance (Einstein famously disagreed with his probabilistic interpretation), his ideas became central to quantum theory. Today, Born’s method remains a cornerstone of quantum mechanics.
Concluding Remarks
The Schrödinger wave equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system evolves over time. By solving this equation, we can predict the behavior of particles at the atomic and subatomic scales, enabling us to tackle real-world problems in physics, chemistry, materials science, engineering, etc.
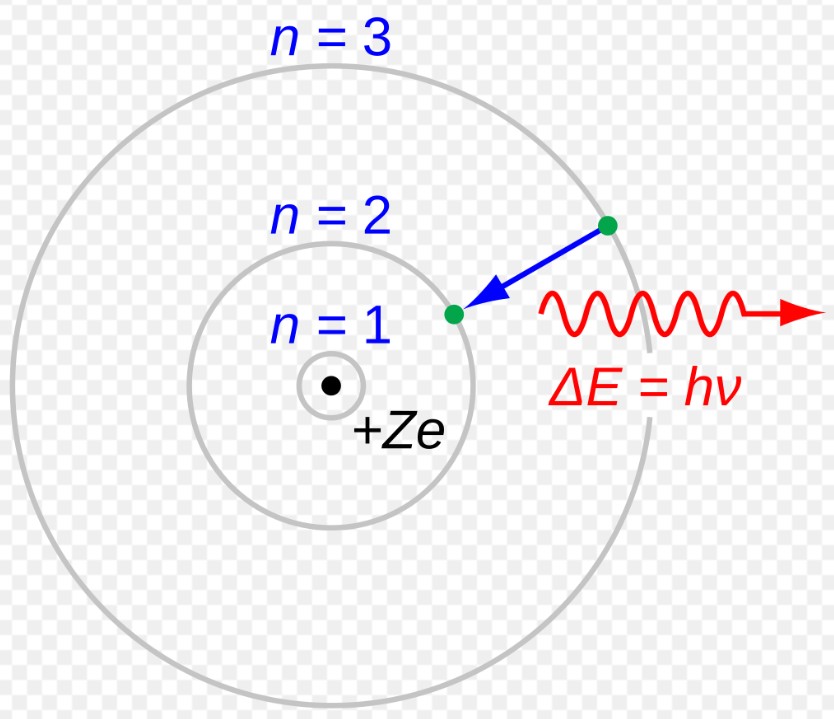
The Schrödinger equation enables us to calculate the allowed energy levels (quantized states) of electrons in atoms and molecules. This has a wide range of applications, like:
- Emission of atom spectra - why atoms emit/absorb light at specific wavelengths (used in spectroscopy, lasers, and LED technology),
- Chemical bonding - How electrons arrange themselves in molecules (crucial for drug design, catalysis, and nanotechnology),
- Predicting material properties. By solving the Schrödinger equation for solids, we can determine electronic band structure - whether a material is a conductor, semiconductor, or insulator (essential for designing solar cells, and microchips),
- Determine magnetic & optical properties - helps in developing new materials for quantum computing, spintronics, and photonics,
- The equation helps simulate how electrons distribute in complex molecules, predicting reactivity and stability (used in drug design and catalysis),
- Quantum simulations - aiding in understanding biochemical processes, leading to better medicines,
- Engineers use the Schrödinger equation to design nanoscale devices with tailored electronic properties (used in displays, sensors, and quantum computers),
- Explains phenomena like scanning tunneling microscopy (STM) and flash memory devices.
- The equation helps model protons and neutrons in nuclei, aiding nuclear energy research,
- Used in quantum field theory to study fundamental particles at accelerators like CERN.
While the Schrödinger equation is exact in principle, solving it for large systems is generally mathematically complicated and computationally expensive. However, approximations like: Density Functional Theory (DFT) (for materials science), Hartree-Fock method (for quantum chemistry), and Quantum Monte Carlo (for high-precision simulations) are used to make calculations feasible.
The Schrödinger equation provides the theoretical foundation for modern technology ranging from semiconductors to medical imaging. By solving it (exactly or approximately), scientists and engineers can manipulate matter at the atomic scale, leading to breakthroughs in computing, energy, medicine, and beyond.

.jpg)